Da vida de Pitágoras quase nada pode ser afirmado com certeza, já que ele foi objeto de uma série de relatos tardios e fantasiosos, como os referentes a viagens e contatos com as culturas orientais. Parece certo, contudo, que o filósofo tenha nascido em 570 a.C. na cidade de Samos.
Fundou uma escola mística e filosófica em Crotona (colônias gregas na península itálica), cujos princípios foram determinantes para a evolução geral da matemática e da filosofia ocidental sendo os principais temas a harmonia matemática, a doutrina dos números e o dualismo cósmico essencial.
Acredita-se que Pitágoras tenha sido casado com a física e matemática grega Theano, que foi sua aluna. Supõe-se que ela e as duas filhas tenham assumido a escola pitagórica após a morte do marido.
Os pitagóricos interessavam-se pelo estudo das propriedades dos números. Para eles, o número, sinônimo de harmonia, constituído da soma de pares e ímpares - os números pares e ímpares expressando as relações que se encontram em permanente processo de mutação -, era considerado como a essência das coisas, criando noções opostas (limitado e ilimitado) e sendo a base da teoria da harmonia das esferas.
Segundo os pitagóricos, o cosmo é regido por relações matemáticas. A observação dos astros sugeriu-lhes que uma ordem domina o universo. Evidências disso estariam no dia e noite, no alterar-se das estações e no movimento circular e perfeito das estrelas. Por isso o mundo poderia ser chamado de cosmos, termo que contém as idéias de ordem, de correspondência e de beleza. Nessa cosmovisão também concluíram que a Terra é esférica, estrela entre as estrelas que se movem ao redor de um fogo central. Alguns pitagóricos chegaram até a falar da rotação da Terra sobre o eixo, mas a maior descoberta de Pitágoras ou dos seus discípulos (já que há obscuridades em torno do pitagorismo, devido ao caráter esotérico e secreto da escola) deu-se no domínio da geometria e se refere às relações entre os lados do triângulo retângulo. A descoberta foi enunciada no teorema de Pitágoras.
Pitágoras foi expulso de Crotona e passou a morar em Metaponto, onde morreu, provavelmente em 496 a.C. ou 497 a.C..
quarta-feira, 16 de novembro de 2011
terça-feira, 8 de novembro de 2011
Aristótelis
Aristóteles
Filósofo grego (384 a.C. - 322 a.C.)
Nascido no reino da Macedônia (norte da Grécia), Aristóteles mudou-se para Atenas aos 17 anos, onde estudou sob a orientação de um dos mais famosos filósofos de todos os tempos: Platão.
A escola dirigida por Platão denominava-se Academia, e Aristóteles nela permaneceu por cerca de vinte anos. Com a morte do mestre, preferiu deixá-la, dizendo-se insatisfeito com a pouca importância que ali vinha sendo dada ao estudo da natureza.
Viajou então por várias parte do mundo grego, que na época era bem mais vasto do que hoje, alcançando, entre outras regiões, o sul da Itália e a Ásia Menor. Foi nesta última região que Aristóteles se fixou por alguns anos. Ali ele se casou e pôde se dedicar a seus estudos preferidos, até ser chamado de volta à sua terra natal.
O novo rei da Macedônia queria que ele cuidasse da educação do seu filho masi velho, tarefa que Aristóteles desempenhou por muitos anos. Só deixou a Macedônia quando seu aluno já tinha sido aclamado rei. Futuramente, ele passaria à história como Alexandre, o Grande, devido a suas conquistas territoriais, que incluiriam não só a própria Atenas, mas também a Pérsia.
Retornando a Atenas, Aristóteles criou sua própria escola, chamada Liceu, além de organizar uma biblioteca de manuscritos.
Quando Alexandre morreu, Aristóteles achou mais prudente deixar a cidade. Temia uma reação dos macedônios contra ele, pois chegou a ser acusado de ofensa religiosa, o que poderia levá-lo a ser condenado à morte (tal como já ocorrera com o ateniense Sócrates meio século antes). Vivendo numa ilha do Mar Egeu, morreria apenas um ano mais tarde.
Os escritos de Aristóteles perfazem grande número de volumes (consta que 150, aproximadamente) e versam sobre assuntos variados: da ciência, política e ética à crítica literária. Desses trabalhos, cerca de dois terços desapareceram. Mesmo os que chegaram até nós ficaram perdidos por séculos, por vezez em mais de uma ocasião. Muitos deles só atravessariam a Idade Média traduzidos para o árabe.
Em seus estudos da natureza, Aritóteles dedicou especial atenção aos seres vivos. Chegou a fazer dissecções em algumas dezenas de espécies animais, classificando cerca de 500 delas de acordo com suas semelhanças e diferenças. Foi o primeiro a considerar que o golfinho não era um peixe, pois possuía placenta, como os mamíferos terrestres. Tal descoberta, porém, seria negada nos séculos seguintes.
Seus critérios de classificação, embora fossem-como era de se esperar-diferentes dos nossos, levaram-no a concluir que haveria na natureza uma hierarquia determinada por modificação nos seres vivos. Só Charles Darwin, em pleno século XIX, voltaria a trabalhar com uma idéia, vigente em sua época, de que tudo na natureza se compunha de quatro elementos - ar, água, fogo, e terra -, mas a eles acrescentou um quinto elemento - o éter -, que formaria o espaço celeste. Concordou também com a idéia dos discípulos de Pitágoras de que a Terra e o céu seriam regidos por diferentes conjuntos de leis, pelas quais a Terra seria mutável e o lugar "natural": a terra ficaria embaixo; sobre ela viria a água, depois o ar e por último, o fogo, que ficaria acima de todos esses elementos.
Por causa dessa ordem "natural", uma pedra (composta principalmente pelo elemento terra) lançada no ar afundaria na água, uma bolha de ar subiria num líquido e o fogo procuraria sempre alcançar o ponto mais alto possível. Isso levou Aristóteles a concluir que, quanto mais pesado um objeto, mais rápido ele desceria e, portanto, os corpos pesados cairiam mais rapidamente que os leves (somente 2000 anos depois Stevin, Galileu e Pascal provariam que essa idéia era falsa).
Para Aristóteles, suas conclusões eram verdadeiras, porque se podia chegar a elas através da argumentação lógica. Apesar de todas as observações que fez, ele considerava que a discussão produzia conclusões mais verdadeiras que os fatos constatados através de experimentos.
De fato, Aristóteles pode ser considerado o criador do estudo da Lógica e seu livro Organon, que trata desse tema, foi o único, dentre toda a sua obra, a continuar sendo estudado na Europa após a queda do Império Romano. Os séculos seguintes não só esqueceriam as contribuições de Aristóteles ao conhecimento da natureza como também viriam a utilizar o que restou de seu trabalho para argumentar contra idéias e descobertas que as novas mentes procurariam divulgar.
De acordo com o site: http://www.hmat.hpg.ig.com.br
domingo, 23 de outubro de 2011
ALBERT EINSTEIN
Einstein nasceu na Alemanha no ano de 1879. Ele foi físico e matemático e até hoje é conhecido pela sua genialidade.
Com sua Teoria da Relatividade mudou o pensamento da humanidade a respeito de tempo e espaço. Esta foi apresentada por ele no ano de 1905, sendo reapresentada com mais informações no ano de 1915. A partir daí, soube-se que era possível criar uma potente arma nuclear.
Em 1921, esta notável figura recebeu o Prêmio Nobel de Física ao explanar sua teoria quântica, que apresentava esclarecimentos sobre o efeito fotoelétrico.
Este brilhante físico e matemático era de origem judia, e, como todo povo judeu, ele foi perseguido pelos nazistas; contudo, ele conseguiu deixar a Alemanha, passando primeiramente pela Inglaterra, e, posteriormente, estabeleceu sua moradia nos Estados Unidos, onde se naturalizou cidadão americano.
Einstein entristeceu-se profundamente ao ver as conseqüências desastrosas da bomba nuclear, e, uma semana antes de sua morte, relatou este fato em uma carta escrita a Bertrand Russel, onde pedia que seu nome fosse colocado numa petição onde clamava para que a produção de armas nucleares fosse abandona.
Este grande homem, que tanto contribuiu com sua genialidade, passou os últimos anos de sua vida em busca de uma teoria onde pudesse trabalhar ao mesmo tempo com a matemática e com as leis da Física. Contudo, sua busca não pôde ser concluída, pois, em 1955, o mundo perdeu este cientista de cérebro brilhante.
http://www.suapesquisa.com/biografias/einstein/
segunda-feira, 17 de outubro de 2011
Johann Carl Friedrich Gauss
Johann Carl Friedrich Gauss (Braunschweig, 30 de Abril de 1777 — Göttingen, 23 de Fevereiro de 1855), foi um matemático, astrônomo e físico alemão. Conhecido como o príncipe dos matemáticos, muitos o consideram o maior gênio da história da matemática. Seu pai, Gerhard Diederich, era jardineiro e pedreiro. Severo e brutal, tudo fez para impedir que seu filho desenvolvesse seu grande potencial.Foi salvo por sua mãe Dorothea e seu tio Friederich que percebeu da inteligência de seu sobrinho.
Tinha memória fotográfica, tendo retido as impressões da infância e da meninice nítidas até a sua morte. Ressentia-se de que seu tio Friederich, um gênio, perdera-se pela morte prematura.
Antes disso já aprendera a ler e a somar sozinho. Aos sete anos entrou para a escola. Segundo uma história famosa, seu diretor, Butner, pediu que os alunos somassem os números inteiros de um a cem. Mal havia enunciado o problema e o jovem Gauss colocou sua lousa sobre a mesa, dizendo: ligget se! Sua resposta, 5050, foi encontrada através do raciocínio que demonstra a fórmula da soma de uma progressão aritmética. Alguns autores argumentam que o problema seria de ordem bastante mais complexa, sugerindo que poderia ser uma soma de uma progressão aritmética como 81097 + 81395 + 81693 + ..... + 110897
Butner ficou tão atônito com a proeza de um menino de dez anos que pagou do próprio bolso livros de aritmética para ele, que os absorvia instantaneamente. Reconhecendo que fora ultrapassado pelo aluno, passou o ensino para seu jovem assistente, Johann Martin Bartels (1769-1856), apaixonado pela matemática. Entre Bartels, com dezessete anos, e o aluno de dez nasceu uma boa amizade que durou toda a vida. Eles estudavam juntos, ajudando-se em suas dificuldades.
O encontro de Gauss com o teorema binômio inspirou-o para alguns de seus maiores trabalhos, tornando-se Gauss o primeiro "rigorista". Insatisfeito com o que ele e Bartels encontravam em seus livros, Gauss foi além, e iniciou a análise matemática.
Nenhum matemático anterior tinha a menor concepção do que é agora aceitável como prova, envolvendo o processo infinito. Ele foi o primeiro a ver que, a "prova" que pode levar a absurdos como "menos 1 é igual ao infinito", não é prova nenhuma. Mesmo que, em alguns casos, uma fórmula dê resultados consistentes, ela não tem lugar na matemática até que a precisa condição sob a qual ela continuará a se submeter tenha sido determinada consistentemente. O rigor imposto por Gauss à análise matemática tornou-a totalmente diferente e superou toda a análise matemática feita por seus antecessores.
sexta-feira, 7 de outubro de 2011
MATEMÁTICOS FAMOSOS EM TODA A HISTORIA
ATENÇÃO A CADA SEMANA FAREMOS UM RESUMO DA VIDA DOS MAIORES E MAIS FAMOSOS MATEMÁTICOS DA HISTÓRIA FIQUEM LIGADOS .
Matemático francês nascido em Vitry, próximo a Paris, que fez carreira profissional na Inglaterra, onde foi professor particular e tornou-se um destacado pesquisador com grandes contribuições foram no campo da teoria das probabilidades, porém sem se tornar professor universitário por causa de sua nacionalidade. Após cinco anos na Academia Protestante em Sedan, foi estudar lógica em Saumur (1682-1684). Indo para Paris, estudou no Collège de Harcourt, mas por causa de sua convicção religiosa fugiu para a Inglaterra (1685) após a revogação do Edito de Nantes e a conseqüente expulsão dos huguenotes.
Foi eleito membro da Royal Society (1697), da Academia de Paris e da de Berlim, nas quais publicou vários trabalhos em seus periódicos. Devido à sua amizade com Newton, integrou a comissão criada pela Royal Society (1710) para esclarecer a paternidade do cálculo entre seu amigo e Leibniz. Pioneiro do desenvolvimento de geometria analítica e a teoria de probabilidade, publicou o célebre Doctrine of Chances (1718), sobre a teoria do acaso, onde expôs a definição de independência estatística junto com muitos problemas com dados e outros jogos. Também pesquisou estatísticas de mortalidade e a fundou a teoria de anuidades.
Outra grande publicação no assunto foi Miscellanea analytica (1730), onde destacou o emprego da trigonometria na probabilidade. Neste livro apresentou uma fórmula injustamente atribuiu a Stirling, na qual ele usou para derivar a curva normal como uma aproximação para o binômio (1733). Na realidade Stirling contribuiu para a melhoria da fórmula na segunda edição do livro (1738). A despeito de sua enorme produção e prestígio nos meios científicos da época morreu em condições de pobreza em Londres.
Abraham de Moivre
Matemático francês nascido em Vitry, próximo a Paris, que fez carreira profissional na Inglaterra, onde foi professor particular e tornou-se um destacado pesquisador com grandes contribuições foram no campo da teoria das probabilidades, porém sem se tornar professor universitário por causa de sua nacionalidade. Após cinco anos na Academia Protestante em Sedan, foi estudar lógica em Saumur (1682-1684). Indo para Paris, estudou no Collège de Harcourt, mas por causa de sua convicção religiosa fugiu para a Inglaterra (1685) após a revogação do Edito de Nantes e a conseqüente expulsão dos huguenotes.
Foi eleito membro da Royal Society (1697), da Academia de Paris e da de Berlim, nas quais publicou vários trabalhos em seus periódicos. Devido à sua amizade com Newton, integrou a comissão criada pela Royal Society (1710) para esclarecer a paternidade do cálculo entre seu amigo e Leibniz. Pioneiro do desenvolvimento de geometria analítica e a teoria de probabilidade, publicou o célebre Doctrine of Chances (1718), sobre a teoria do acaso, onde expôs a definição de independência estatística junto com muitos problemas com dados e outros jogos. Também pesquisou estatísticas de mortalidade e a fundou a teoria de anuidades.
Outra grande publicação no assunto foi Miscellanea analytica (1730), onde destacou o emprego da trigonometria na probabilidade. Neste livro apresentou uma fórmula injustamente atribuiu a Stirling, na qual ele usou para derivar a curva normal como uma aproximação para o binômio (1733). Na realidade Stirling contribuiu para a melhoria da fórmula na segunda edição do livro (1738). A despeito de sua enorme produção e prestígio nos meios científicos da época morreu em condições de pobreza em Londres.
quinta-feira, 2 de junho de 2011
Numeros complexos
Quantas vezes, ao calcularmos o valor de Delta (b2- 4ac) na resolução da equação do 2º grau, nos deparamos com um valor negativo (Delta < 0). Nesse caso, sempre dizemos ser impossível a raiz no universo considerado (normalmente no conjunto dos reais- R). A partir daí, vários matemáticos estudaram este problema, sendo Gauss e Argand os que realmente conseguiram expor uma interpretação geométrica num outro conjunto de números, chamado de números complexos, que representamos por C.
Números Complexos
Chama-se conjunto dos números complexos, e representa-se por C, o conjunto de pares ordenados, ou seja:
z = (x,y)
onde x pertence a R e y pertence a R.
onde x pertence a R e y pertence a R.
Então, por definição, se z = (x,y) = (x,0) + (y,0)(0,1) onde i=(0,1), podemos escrever que:
z=(x,y)=x+yi
Exemplos:
(5,3)=5+3i
(2,1)=2+i
(-1,3)=-1+3i ...
Dessa forma, todo o números complexo z=(x,y) pode ser escrito na forma z=x+yi, conhecido como forma algébrica, onde temos:
(5,3)=5+3i
(2,1)=2+i
(-1,3)=-1+3i ...
Dessa forma, todo o números complexo z=(x,y) pode ser escrito na forma z=x+yi, conhecido como forma algébrica, onde temos:
x=Re(z, parte real de z
y=Im(z), parte imaginária de z
y=Im(z), parte imaginária de z
Igualdade entre números complexos
Dois números complexos são iguais se, e somente se, apresentam simultaneamente iguais a parte real e a parte imaginária. Assim, se z1=a+bi e z2=c+di, temos que:
Dois números complexos são iguais se, e somente se, apresentam simultaneamente iguais a parte real e a parte imaginária. Assim, se z1=a+bi e z2=c+di, temos que:
z1=z2<==> a=c e b=d
Adição de números complexos
Para somarmos dois números complexos basta somarmos, separadamente, as partes reais e imaginárias desses números. Assim, se z=a+bi e z2=c+di, temos que:
Para somarmos dois números complexos basta somarmos, separadamente, as partes reais e imaginárias desses números. Assim, se z=a+bi e z2=c+di, temos que:
z1+z2=(a+c) + (b+d)
Subtração de números complexos
Para subtrairmos dois números complexos basta subtrairmos, separadamente, as partes reais e imaginárias desses números. Assim, se z=a+bi e z2=c+di, temos que:
Para subtrairmos dois números complexos basta subtrairmos, separadamente, as partes reais e imaginárias desses números. Assim, se z=a+bi e z2=c+di, temos que:
z1-z2=(a-c) + (b-d)
Potências de i
Se, por definição, temos que i = - (-1)1/2, então:
i0 = 1
i1 = i
i2 = -1
i3 = i2.i = -1.i = -i
i4 = i2.i2=-1.-1=1
i5 = i4. 1=1.i= i
i6 = i5. i =i.i=i2=-1
i7 = i6. i =(-1).i=-i ......
Observamos que no desenvolvimento de in (n pertencente a N, com n variando, os valores repetem-se de 4 em 4 unidades. Desta forma, para calcularmos in basta calcularmos ir onde r é o resto da divisão de n por 4.
Exemplo:
i63 => 63 / 4 dá resto 3, logo i63=i3=-i
Multiplicação de números complexos
Para multiplicarmos dois números complexos basta efetuarmos a multiplicacão dois dois binômios, observando os valores das potência de i. Assim, se z1=a+bi e z2=c+di, temos que:
Se, por definição, temos que i = - (-1)1/2, então:
i0 = 1
i1 = i
i2 = -1
i3 = i2.i = -1.i = -i
i4 = i2.i2=-1.-1=1
i5 = i4. 1=1.i= i
i6 = i5. i =i.i=i2=-1
i7 = i6. i =(-1).i=-i ......
Observamos que no desenvolvimento de in (n pertencente a N, com n variando, os valores repetem-se de 4 em 4 unidades. Desta forma, para calcularmos in basta calcularmos ir onde r é o resto da divisão de n por 4.
Exemplo:
i63 => 63 / 4 dá resto 3, logo i63=i3=-i
Multiplicação de números complexos
Para multiplicarmos dois números complexos basta efetuarmos a multiplicacão dois dois binômios, observando os valores das potência de i. Assim, se z1=a+bi e z2=c+di, temos que:
z1.z2 = a.c + adi + bci + bdi2
z1.z2= a.c + bdi2 = adi + bci
z1.z2= (ac - bd) + (ad + bc)i
Observar que : i2= -1
z1.z2= a.c + bdi2 = adi + bci
z1.z2= (ac - bd) + (ad + bc)i
Observar que : i2= -1
Conjugado de um número complexo
Dado z=a+bi, define-se como conjugado de z (representa-se por z-) ==> z-= a-bi
Exemplo:
z=3 - 5i ==> z- = 3 + 5i
z = 7i ==> z- = - 7i
z = 3 ==> z- = 3
Divisão de números complexos
Para dividirmos dois números complexos basta multiplicarmos o numerador e o denominador pelo conjugado do denominador. Assim, se z1= a + bi e z2= c + di, temos que:
z1 / z2 = [z1.z2-] / [z2z2-] = [ (a+bi)(c-di) ] / [ (c+di)(c-di) ]
Módulo de um número complexo
Dado z = a+bi, chama-se módulo de z ==> | z | = (a2+b2)1/2, conhecido como ro
Interpretação geométrica
Como dissemos, no início, a interpretação geométrica dos números complexos é que deu o impulso para o seu estudo. Assim, representamos o complexo z = a+bi da seguinte maneira
Dado z=a+bi, define-se como conjugado de z (representa-se por z-) ==> z-= a-bi
Exemplo:
z=3 - 5i ==> z- = 3 + 5i
z = 7i ==> z- = - 7i
z = 3 ==> z- = 3
Divisão de números complexos
Para dividirmos dois números complexos basta multiplicarmos o numerador e o denominador pelo conjugado do denominador. Assim, se z1= a + bi e z2= c + di, temos que:
z1 / z2 = [z1.z2-] / [z2z2-] = [ (a+bi)(c-di) ] / [ (c+di)(c-di) ]
Módulo de um número complexo
Dado z = a+bi, chama-se módulo de z ==> | z | = (a2+b2)1/2, conhecido como ro
Interpretação geométrica
Como dissemos, no início, a interpretação geométrica dos números complexos é que deu o impulso para o seu estudo. Assim, representamos o complexo z = a+bi da seguinte maneira

Da interpretação geométrica, temos que:

que é conhecida como forma polar ou trigonométrica de um número complexo.
Operações na forma polar
Sejam z1=ro1(cos t11) e z2=ro1(cos t1+i sent1). Então, temos que:
a)Multiplicação

sábado, 28 de maio de 2011
A maior parte dos estudantes vêem o ensino da Matemática como uma das matérias mais difíceis e menos atraentes. Mal se dão conta de que todos fazem uso da Matemática no dia-a-dia. Em casa, no trabalho, no supermercado, no esporte. No futebol, além do tempo do jogo, há a quantidade de jogadores, a probabilidade de ganho ou perda nos campeonatos com os pontos adquiridos nos jogos. O cidadão se depara com situações que exigem raciocínio matemático como adição, subtração, divisão e multiplicação. E não somente as quatro operações básicas que aparecem no cotidiano. Muitas vezes, as pessoas acabam fazendo cálculos complexos para resolver situações do dia-a-dia e nem percebem que estão praticando a Matemática. Por isso, na sala de aula a metodologia do Projeto Cidade Júnior facilita o aprendizado dos conteúdos curriculares, pois possibilita ao educador contextualizar os conhecimentos abstratos da Matemática, através da aproximação da realidade em relação aos conteúdos, identificando o uso desse conhecimento na sociedade. Miyoko S. Yamada – Matemática
sexta-feira, 6 de maio de 2011
Curiosidades
O epitáfio de Diofanto
Diofanto foi um matemático que viveu em Alexandria no século 3º. Foi o primeiro matemático grego a usar simbolismo algébrico e sua obra nos chegou através de fragmentos do seu livro "Aritmética". Em sua homenagem, chamamos de equações diofantinas as equações cujas soluções devem ser números inteiros.
Pouco sabemos sobre sua vida, mas existe uma charada que, dizem, teria sido gravada no seu túmulo: "Aqui jaz o matemático que passou um sexto da sua vida como menino. Um dozeavo da sua vida passou como rapaz. Depois viveu um sétimo da sua vida antes de se casar. Cinco anos após nasceu seu filho, com quem conviveu metade da sua vida. Depois da morte de seu filho, sofreu mais 4 anos antes de morrer." Quantos anos viveu Diofanto?
Pouco sabemos sobre sua vida, mas existe uma charada que, dizem, teria sido gravada no seu túmulo: "Aqui jaz o matemático que passou um sexto da sua vida como menino. Um dozeavo da sua vida passou como rapaz. Depois viveu um sétimo da sua vida antes de se casar. Cinco anos após nasceu seu filho, com quem conviveu metade da sua vida. Depois da morte de seu filho, sofreu mais 4 anos antes de morrer." Quantos anos viveu Diofanto?
O último teorema de Fermat
Pierre de Fermat foi um grande matemático francês do século 17. Um dia, Fermat estava lendo um livro, "Aritmética" de Diofanto, onde o autor discutia as soluções inteiras para uma equação do tipo x² + y² = z². De acordo com o Teorema de Pitágoras, esses números constituem os lados de um triângulo retângulo. Existem infinitos números inteiros que satisfazem essa equação, como 3, 4 e 5 ou 5, 12 e 13.
Fermat começou a pensar se o mesmo seria verdadeiro para cubos ou biquadrados (quarta potência), isto é, se existiriam também soluções inteiras para equações do tipo x^3 + y^3 = z^3 ou, x^4 + y^4 = z^4 de modo geral, x^n + y^n = z^n. Ele escreveu na margem do seu livro: "É impossível separar um cubo em dois, ou um biquadrado em dois, ou, de um modo geral qualquer potência, exceto o quadrado, em duas potências com o mesmo expoente. Descobri uma demonstração demasiadamente maravilhosa, mas é demasiadamente comprida para caber nesta margem."Fermat morreu sem apresentar a demonstração Com isso, criou-se um problema que desafiaria os maiores matemáticos do mundo durante mais de três séculos e meio. Euler, o maior matemático do século 18, teve que reconhecer sua derrota. Recentemente, grandes matemáticos como Elkies e Faltings, quase o demonstraram. Muitos matematicos modernos começaram a duvidar que Fermat tivesse realmente demonstrado esse teorema. Até que, em 1995, um matemático americano, Andrew Wiles demonstrou definivamente o último teorema de Fermat, consagrando-se mundialmente.
Fermat começou a pensar se o mesmo seria verdadeiro para cubos ou biquadrados (quarta potência), isto é, se existiriam também soluções inteiras para equações do tipo x^3 + y^3 = z^3 ou, x^4 + y^4 = z^4 de modo geral, x^n + y^n = z^n. Ele escreveu na margem do seu livro: "É impossível separar um cubo em dois, ou um biquadrado em dois, ou, de um modo geral qualquer potência, exceto o quadrado, em duas potências com o mesmo expoente. Descobri uma demonstração demasiadamente maravilhosa, mas é demasiadamente comprida para caber nesta margem."Fermat morreu sem apresentar a demonstração Com isso, criou-se um problema que desafiaria os maiores matemáticos do mundo durante mais de três séculos e meio. Euler, o maior matemático do século 18, teve que reconhecer sua derrota. Recentemente, grandes matemáticos como Elkies e Faltings, quase o demonstraram. Muitos matematicos modernos começaram a duvidar que Fermat tivesse realmente demonstrado esse teorema. Até que, em 1995, um matemático americano, Andrew Wiles demonstrou definivamente o último teorema de Fermat, consagrando-se mundialmente.
Você é capaz de somar os algarismos de 1 a 100 em poucos minutos?
Carl Friedrich Gauss (1777-1855) aos 10 anos de idade respondeu rapidamente 5.050 ao seu professor surpreendendo-o pela sua grande habilidade na matemática. Em 1792, seu talento foi reconhecido pelo duque de Braunschweig, que lhe garantiu recursos para prosseguir o estudo de matemática. Gauss criou a geometria diferencial, e fez novas descobertas como a Lei da Reciprocidade Quadrática, que introduz o conceito de congruência e o Teorema Fundamental da Álgebra. Em 1801, publicou Disquisitiones Arithmeticae, seu tratado sobre a Teoria dos Números. No mesmo ano, calculou a órbita do asteróide Ceres. Com base em uma teoria que desenvolveu, previu corretamente onde e quando o Ceres deveria reaparecer. Morreu em 23 de fevereiro de 1855, sendo considerado o "Príncipe da Matemática".
Vejam abaixo a resolução proposta por Gauss
(isso aos 10 anos de idade):
(isso aos 10 anos de idade):
 |
Revolução Matemática - O cálculo diferencial e integral
O cálculo diferencial e integral, que Newton desenvolve ao mesmo tempo que o alemão Wilheim Leibniz (1646-1716), revoluciona a matemática. Para se saber a área de um círculo, utilizando a nova ferramenta, basta dividir esse círculo em quadrados iguais, bem pequenos. Em seguida, calcula-se a área de um quadrado e multiplica-se pelo número total de quadrados. Com isso, acha-se a área (ou o volume se for o caso, de qualquer figura). Os quadrados têm de ser infinitamente pequenos para encher toda a borda do círculo, e o número de quadrados precisa ser infinito. Portanto, a área total será uma soma de infinitos termos, tipo de soma que os gregos já sabiam fazer há mais de 2 mil anos.
Você sabia?
Que o maior número primo conhecido é , que tem 2.098.960 dígitos e foi descoberto em 01/06/1999 por Nayan Hafratwala, um participante do GIMPS, um projeto cooperativo para procurar primos de mersenne.
, que tem 2.098.960 dígitos e foi descoberto em 01/06/1999 por Nayan Hafratwala, um participante do GIMPS, um projeto cooperativo para procurar primos de mersenne.
Você sabia?
Que o maior número primo conhecido é
 , que tem 2.098.960 dígitos e foi descoberto em 01/06/1999 por Nayan Hafratwala, um participante do GIMPS, um projeto cooperativo para procurar primos de mersenne.
, que tem 2.098.960 dígitos e foi descoberto em 01/06/1999 por Nayan Hafratwala, um participante do GIMPS, um projeto cooperativo para procurar primos de mersenne. Que são conhecidos 51539600000 casas decimais de  (Pi), calculadas por Y. Kamada e D. Takahashi, da Universidade de Tokio em 1997? E que em 21/08/1998 foi calculada pelo projeto Pihex a 5000000000000a. casa binária de (Pi).
(Pi), calculadas por Y. Kamada e D. Takahashi, da Universidade de Tokio em 1997? E que em 21/08/1998 foi calculada pelo projeto Pihex a 5000000000000a. casa binária de (Pi).
 (Pi), calculadas por Y. Kamada e D. Takahashi, da Universidade de Tokio em 1997? E que em 21/08/1998 foi calculada pelo projeto Pihex a 5000000000000a. casa binária de (Pi).
(Pi), calculadas por Y. Kamada e D. Takahashi, da Universidade de Tokio em 1997? E que em 21/08/1998 foi calculada pelo projeto Pihex a 5000000000000a. casa binária de (Pi).Fonte :http://www.exatas.mat.br/curiosidades.htm
Geometria analítica
1 - Introdução
A Geometria Analítica é uma parte da Matemática , que através de processos particulares , estabelece as relações existentes entre a Álgebra e a Geometria. Desse modo , uma reta , uma circunferência ou uma figura podem ter suas propriedades estudadas através de métodos algébricos .
Os estudos iniciais da Geometria Analítica se deram no século XVII , e devem-se ao filósofo e matemático francês René Descartes (1596 - 1650), inventor das coordenadas cartesianas (assim chamadas em sua homenagem), que permitiram a representação numérica de propriedades geométricas. No seu livro Discurso sobre o Método, escrito em 1637, aparece a célebre frase em latim "Cogito ergo sum" , ou seja: "Penso, logo existo".
Os estudos iniciais da Geometria Analítica se deram no século XVII , e devem-se ao filósofo e matemático francês René Descartes (1596 - 1650), inventor das coordenadas cartesianas (assim chamadas em sua homenagem), que permitiram a representação numérica de propriedades geométricas. No seu livro Discurso sobre o Método, escrito em 1637, aparece a célebre frase em latim "Cogito ergo sum" , ou seja: "Penso, logo existo".
1.1 - Coordenadas cartesianas na reta
Seja a reta r na Fig. abaixo e sobre ela tomemos um ponto O chamado origem.
Adotemos uma unidade de medida e suponhamos que os comprimentos medidos a partir de O, sejam positivos à direita e negativos à esquerda.
Adotemos uma unidade de medida e suponhamos que os comprimentos medidos a partir de O, sejam positivos à direita e negativos à esquerda.
O comprimento do segmento OA é igual a 1 u.c (u.c = unidade de comprimento). É fácil concluir que existe uma correspondência um a um (correspondência biunívoca) entre o conjunto dos pontos da reta e o conjunto R dos números reais. Os números são chamados abscissas dos pontos. Assim, a abscissa do ponto A’ é -1, a abscissa da origem O é 0, a abscissa do ponto A
é 1, etc.
A reta r é chamada eixo das abscissas.
Fonte: http://www.algosobre.com.br/matematica/geometria-analitica.html
é 1, etc.
A reta r é chamada eixo das abscissas.
Fonte: http://www.algosobre.com.br/matematica/geometria-analitica.html
sábado, 30 de abril de 2011
GRANDES GÊNIOS DA MATEMÁTICA
Isaac Newton:
Em um dia ensolarado, Newton descansava deitado embaixo de uma macieira, quando de repente uma maça caiu ao seu lado, e, num momento de inspiração, ele formulou a Lei da Gravitação Universal, conhecida e estudada até hoje.
Isaac Newton era grande discípulo de Galileu Galilei, que morreu no ano do nascimento de Newton, e conhecia todas as suas teorias. Após este acontecimento, Newton passou a formular outras leis, como a de Ação e Reação, que diz: "Toda ação produzirá uma reação, de igual intensidade mas de sentidos opostos". Outra lei famosa é a da inércia, tendência que os corpos têm de manter sua velocidade. Também foi ele quem deduziu que a força peso é o produto da massa de um corpo multiplicada pelo valor da aceleração da gravidade.
Além da Física, Newton era um estudioso em outras áreas de conhecimento, como a Matemática, na qual contribuiu com, por exemplo, as funções logarítmicas e os seus binômios. O aprofundamento nesses cálculos se deu ao fato de não haver "matemática suficiente" para explicar suas descobertas.
Newton trocou correspondências com outros cientistas e inventores de sua época, como, por exemplo Kepler e também Leonardo Da Vinci.
Galileu é considerado o pai da Física, porém foi Isaac Newton quem deu uma das maiores contribuições para a continuação desta ciência. A Física só é o que é hoje graças a ele.
Albert Einstein:
O mais célebre dos cientistas do século XX, responsável por teorias que revolucionaram não apenas a física, mas o próprio pensamento humano, Einstein acreditava que só a evolução moral impediria uma catástrofe a nível planetário.
Albert Einstein nasceu na cidade alemã de Ulm, em 14 de março de 1879. Filho de um pequeno industrial judeu, iniciou os estudos em Munique e cedo se destacou no estudo da matemática, física e filosofia. Ainda na infância, incentivado pela mãe, começou a estudar violino, instrumento que o acompanharia ao longo da vida. Com o objetivo de tornar-se professor, concluiu o curso de graduação no Instituto Politécnico de Zurique, em 1900, época em que já dedicava a maior parte de seu tempo ao estudo da física teórica. Obteve nessa época a cidadania suíça e, não tendo conseguido colocação na universidade, aceitou um lugar no departamento de patentes em Berna.
Em 1905, ano em que concluiu o doutorado, Einstein publicou quatro ensaios científicos, cada um deles com uma grande descoberta no campo da física. No primeiro, fez uma análise teórica do movimento browniano, produzido pelo choque das partículas de um líquido sobre corpos microscópicos nele introduzidos; no segundo, formulou uma nova teoria da luz, com o importante conceito de fóton, baseando-se na teoria quântica proposta em 1900 pelo físico Max Planck; no terceiro, expôs a formulação inicial da teoria da relatividade e no quarto e último trabalho, propôs uma fórmula para a equivalência entre massa e energia, a célebre equação E = mc², pela qual a energia E de uma quantidade de matéria, com massa m, é igual ao produto da massa pelo quadrado da velocidade da luz, representada por c.
Descoberta da relatividade.
No ensaio dedicado à relatividade, intitulado "Elektrodynamik Bewegter Körper" ("Movimento eletrodinâmico dos corpos"), o cientista afirma que espaço e tempo são valores relativos e não absolutos, ao contrário do que se acreditava até então. Afirma ainda ser a da luz a velocidade máxima no universo e acrescenta: para o corpo que se deslocasse a essa velocidade, o tempo sofreria uma dilatação, ao mesmo tempo em que se registraria uma contração do espaço. Assim, o corpo que permanecesse em repouso envelheceria em relação ao outro corpo, em movimento.
Cada vez mais respeitado no meio acadêmico, Einstein ensinou em Berna, Zurique e Praga, entre os anos de 1909 e 1913. Foi então convidado a ocupar uma cátedra na Universidade de Berlim, que pouco depois acumulou com a direção do respeitado Instituto Kaiser Wilhelm. Nessa época, sua grande preocupação era a generalização da teoria da relatividade, com a elaboração de uma nova teoria capaz de interpretar, por meio de considerações semelhantes, o campo eletromagnético e o campo gravitacional, que acabaria por receber a denominação de teoria do campo unificado. Em 1916, o cientista publicou Grundlage der allgemeinen Relativitätstheorie (Fundamento geral da teoria da relatividade), formulação final da teoria geral da relatividade. Nesse mesmo ano, passou a manifestar uma preocupação com os problemas sociais que o acompanharia ao longo de toda a sua carreira.
Em 1919, Einstein tornou-se conhecido em todo o mundo, depois que sua teoria foi comprovada em experiência realizada durante um eclipse solar. Por essa época começou a viajar pelo mundo, não apenas para expor suas teorias físicas, mas também para debater problemas como o racismo e a paz mundial. Uma dessas viagens o traria ao Brasil, em 1925. Em 1921, foi agraciado com o Prêmio Nobel de física e indicado para integrar a Organização de Cooperação Intelectual da Liga das Nações. No mesmo ano, publicou Über die spezielle und allgemeine Relativitätstheorie gemeinverständlich (Sobre a teoria da relatividade especial e geral), obra de divulgação.
A noção de equivalência entre massa e energia, a do continuum quadridimensional e outras descobertas de Einstein provocaram uma verdadeira renovação do pensamento humano, num período de grande fertilidade intelectual, com interpretações filosóficas das mais diversas tendências. Os resultados de suas descobertas foram utilizados como argumento tanto pelos defensores do empirismo de total rigor lógico quanto pelos adeptos do idealismo matemático, segundo o qual o universo pode ser reduzido à abstração das fórmulas e das relações numéricas.
Bomba atômica e pacifismo.
Em 1933, um ano após visitar universidades e instituições de pesquisas nos Estados Unidos, Einstein renunciou a seus cargos na Alemanha, onde os nazistas já estavam no poder, e fixou residência em território americano. Passou a ensinar no Instituto de Estudos Avançados da Universidade de Princeton, do qual se tornaria diretor. Em 1940 adotou a cidadania americana.
Durante esse período, o desenvolvimento de armas nucleares e as manifestações cada vez mais freqüentes de racismo no mundo constituíram as principais preocupações de Einstein. Os físicos alemães Otto Hahn e Lise Meitner tinham descoberto como provocar artificialmente a fissão do urânio. Na Itália, as pesquisas de Enrico Fermi indicavam ser possível provocar uma reação em cadeia, com a liberação de um número cada vez maior de átomos de urânio e, em conseqüência, de enorme quantidade de energia. Fermi, que acabara de chegar aos Estados Unidos, e os físicos húngaros Leo Szilard e Eugene Wigner pediram então a Einstein que entrasse em contato com a Casa Branca. Ele escreveu então uma carta ao presidente Franklin Roosevelt em que alertava para o risco que significaria para a humanidade a utilização pelos nazistas da tecnologia nuclear na fabricação de armas de grande poder destrutivo. Logo após receber a mensagem, o chefe de estado americano deu início ao projeto Manhattan, que tornou os Estados Unidos pioneiros no aproveitamento da energia atômica em todo o mundo e resultou na fabricação da primeira bomba atômica.
Embora não tivesse participado do projeto e sequer soubesse que uma bomba atômica tinha sido construída até que Hiroxima fosse arrasada, em 1945, o nome de Einstein passou para a história associado ao advento da era atômica. Durante a segunda guerra mundial, ele participou da organização de grupos de apoio aos refugiados e, terminado o conflito, após o lançamento de bombas atômicas em Hiroxima e Nagasaki, uniu-se a outros cientistas que lutavam para evitar nova utilização da bomba. Intensificando a militância pacifista, defendeu particularmente o estabelecimento de uma organização mundial de controle sobre as armas atômicas. Em 1945, renunciou ao cargo de diretor do Instituto de Estudos Avançados da Universidade de Princeton, mas continuou a trabalhar naquela instituição.
A intensa atividade intelectual de Einstein resultou na publicação de grande número de trabalhos, entre os quais vale destacar Warum Krieg? (1933; Por que a guerra?), em colaboração com Sigmund Freud; Mein Weltbild (1949; O mundo como eu o vejo); e Out of My Later Years (1950; Meus últimos anos). A principal característica de sua obra foi uma síntese do conhecimento sobre o mundo físico, que acabou por levar a uma compreensão mais abrangente e mais profunda do universo. Suas descobertas tornaram possível entender o comportamento das partículas animadas de grande velocidade e suas respectivas leis. Os princípios da relatividade revolucionaram a física newtoniana, pois, com o emprego de aceleradores, tornou-se possível obter partículas animadas de enorme velocidade, cuja mecânica em muito se afasta das leis newtonianas.
Einstein conseguiu reduzir as leis da mecânica e harmonizá-las com aquelas que regem as propriedades dos campos eletromagnéticos. Com sua concepção de fóton, permitiu que mais tarde se fundissem, na teoria ondulatória de Louis de Broglie, a mecânica e o eletromagnetismo, o que no século anterior parecia impossível. Albert Einstein morreu em Princeton, em 18 de abril de 1955.
Outros:
-
DANIEL GABRIEL FAHRENHEIT (1686-1736), físico alemão: começou a construir seus próprios termômetros após uma visita ao astrônomo dinamarquês Olaf Roemer (1644-1710), e, em 1714, passou a usar mercúrio como substância termométrica. Em 1724 criou a escala que leva seu nome, sendo 32 o valor atribuído para a fusão da água e 212 para a sua ebulição;
-
ANDERS CELSIUS (1701-1744), astrônomo e físico sueco: em 1742, apresentou à Real Sociedade sueca sua escala, que adotava 0 para a ebulição da água e 100 para sua fusão. Em 1745, o biólogo Carlos Lineu (1707-1778) propôs a inversão desses valores, sendo 0 para fusão e 100 para ebulição. A adoção da escala Celsius ocorreu apenas em 1948;
-
ANTOINE-LAURENT LAVOISIER (1743-1794), químico francês: explicou a combustão, como sendo uma simples reação com o oxigênio. Introduziu o termo "calórico" para descrever o elemento imponderável responsável pelo aquecimento dos corpos, por algumas reações químicas, etc. Junto com Pierre-Simon Laplace (1749-1827), fez importantes estudos sobre o calor liberado na combustão. Morreu guilhotinado;
-
CHRISTIAN HUYGENS (1629-1695), físico holandês: propôs a teoria ondulatória para explicar a natureza da luz, na qual afirma que ela se propaga por meio de ondas, do mesmo modo que o som. Mas o som não se propaga no vácuo, e a luz sim, para explicar isto, Huygens imaginou um meio elástico e imponderável a que chamou de "éter";
-
JAMES CLERCK MAXWELL (1831-1879), físico escocês: aperfeiçoou a teoria de Huygens e formulou a teoria ondulatória magnética, na qual afirma que a luz é constituída pelas denominadas ondas eletromagnéticas. Assim resolveu-se o problema da propagação da luz no vácuo, já que essas ondas podem fazê-lo porque são geradas de variações de campo elétrico e de campo magnético;
-
HEINRICH-RUDOLF HERTZ (1857-1894), físico alemão: descobriu e efeito fotoelétrico, em 1887, pelo qual, em certas condições, a luz pode arrancar elétrons da superfície de um metal. Essa efeito não é explicável pela teoria ondulatória. Este efeito foi explicado pelo renomado físico alemão Albert Einstein (1879-1955), ele imaginava que a luz e toda radiação eletromagnética é emitida ou absorvida de modo descontínuo;
-
BENJAMIM FRANKLIN (1706-1790), cientista e político americano: após muitas experiências de outros cientistas, foi quem deu o impulso definitivo para a ciência elétrica, não apenas pela invenção do pára-raios, mas especialmente por suas pesquisas e conceitos no campo da eletricidade;
-
CHARLES AUGUSTIN DE COULOMB (1736-1806), cientista francês: realizou os primeiros estudos quantitativos sobre as ações entre corpos eletricamente carregados. Estabeleceu também uma lei que leva o seu nome, através da utilização de uma balança de torção;
-
ALESSANDRO VOLTA (1745-1827), físico italiano: construiu sua pilha elétrica no início do século XIX, tendo início, a partir daí, a fase mais importante da eletricidade, com a obtenção das cargas elétricas em movimento, o que deu-se o nome de corrente elétrica;
-
GEORG SIMON OHM (1787-1854), físico alemão: introduziu o conceito de resistência elétrica e enunciou a lei que leva seu nome. Também foi graças a ele que os estudos sobre corrente elétrica tiveram grande evolução;
-
CLAUDE POUILLET (1790-1868), físico francês: responsável pela lei que permite determinar a intensidade da corrente num circuito simples. Tiveram também grande destaque nas experiências com circuitos elétricos o inglês Charles Wheatstone (1802-1875) e o alemão Gustav Robert Kirchhoff (1824-1887);
-
THOMAS ALVA EDISON (1847-1930), inventor norte-americano: contribuiu bastante para as aplicações práticas da eletricidade, muitas essenciais para a construção do mundo tecnológico em que vivemos. Pode-se citar, dentre uma de suas invenções, a lâmpada elétrica, o microfone, o projetor cinematográfico e o aperfeiçoamento do telefone (inventado por Graham Bell);
-
CHRISTIAN OERSTED (1771-1851), físico dinamarquês: verificou que, ao colocar uma bússola sob um fio elétrico, a agulha desviava quando se fazia passar uma corrente pelo fio. A partir desse fato, estabeleceu-se a conexão entre corrente elétrica e os fenômenos magnéticos. Nascia aí o Eletromagnetismo;
Existem muitos outros cientistas e físicos que não foram citados acima, veja uma lista deles:
Brahe | Torricelli | Gilbert | Henry | Lens | Ampère | Planck |
Fonte : http://www.sobrefisica.hpg.ig.com.br/g_genios.htm
quinta-feira, 28 de abril de 2011
Progressão geométrica (PG0
Fórmula da seqüência numérica
Carlos Alberto Campagner*
Especial para a Página 3 Pedagogia & Comunicação
Assim como a progressão aritmética, a progressão geométrica (PG) é uma maneira de estabelecer uma seqüência de números. Neste caso, no entanto, em vez de uma soma como elemento constante, temos uma múltiplicação.Especial para a Página 3 Pedagogia & Comunicação
Imagine uma progressão em que a lei de formação seja a multiplicação do termo anterior por um número. A progressão com esta lei de formação chama-se Progressão Geométrica ou P.G.. Exemplo:
(2,4,8,16,32,64,...)
O quociente entre dois números consecutivos é igual a 2.
 |
Fórmula da PG: do enésimo termo
Pela definição de PG, a fórmula de um termo é: |
Logo pode-se deduzir que para um termo qualquer
 :
:(*)
 |
Fórmula da soma de um a P.G.
Como não temos o gênio de Gauss, que descobriu a fórmula das Progressões Aritméticas num estalo, a dedução da fórmula da soma de uma P.G. é um pouco mais trabalhosa.Em uma P.G.
 a soma dos n primeiros termos será:
a soma dos n primeiros termos será:(**)
 |
Multiplicando-se os dois termos por q tem-se:
 |
Como
 |
Tem-se
(***)
 |
Fazendo (**) menos (***) obtemos:
 |
Como de (*)
 |
Logo:
 |
para
 (pois é óbvio que com q = 1 não existe P.G.)
(pois é óbvio que com q = 1 não existe P.G.)Uma curiosidade:
Conta a lenda que o inventor do jogo de xadrez foi agraciado pelo rei por sua invenção com um pedido. O inventor pediu pouca coisa:1 grão de trigo para a primeira casa do tabuleiro de xadrez,
2 grãos pela segunda casa,
4 grãos pela terceira casa,
8 grãos pela quarta casa
e assim sucessivamente até a 64º do tabuleiro.
Será que ele pediu pouca coisa?
 |
O resultado é nada menos que18.446.744.073.709.551.615 grãos... ou seja, dezoito quintilhões, quatrocentos e quarenta e seis quatrilhões, setecentos e quarenta e quatro trilhões, setenta e três bilhões, setecentos e nove milhões, quinhentos e cinqüenta e um mil, seiscentos e quinze grãos
quinta-feira, 14 de abril de 2011
Progressão Aritmética
Interpolação Aritmética
É a ação de inserir ou interpolar uma quantidade de meios aritméticos entre extremos de uma progressão aritmética. A fórmula utilizada é:
Onde: Un=U1+(n-1).r
- un = Último termo da P.A.
- u1 = Primeiro termo da P.A.
- n = Número total de termos da P.A.
- r = Razão da P.A.
Tipos de progressões aritméticas
Progressão aritmética constante
Uma progressão aritmética constante ou estacionária é toda progressão aritmética em que todos os termos são iguais, sendo que para isso a razão r tem que ser sempre igual a zero.
Exemplos de progressão aritmética constante:
- P.A. (5,5,5,5,5,5,5,5,5,...) - razão r = 0
- P.A. (0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,...) - razão r = 0
Progressão aritmética crescente
Uma progressão aritmética crescente é toda progressão aritmética em que cada termo, a partir do segundo, é maior que o termo que o antecede, sendo que para isso a razão r tem que ser sempre maior que zero (r>0).
Exemplos de progressão aritmética crescente:
- P.A. (2,4,6,8,10,12,14,16,18,20,22,24,26,28,30,32,...) - razão r = 2
- P.A. (3,6,9,12,15,18,21,24,27,30,33,36,39,42,45,...) - razão r = 3
Progressão aritmética decrescente
Uma progressão aritmética decrescente é toda progressão aritmética em que cada termo, a partir do segundo, é menor que o termo que o antecede, sendo que para isso a razão r tem que ser sempre menor do que zero (r<0).
Exemplos de progressão aritmética decrescente:
- P.A. (6,4,2,0,-2,-4,-6,-8,-10,-12,-14,-16,-18,-20,-22,-24,-26,-28,...) - razão r = -2
- P.A. (6,3,0,-3,-6,-9,-12,-15,-18,-21,-24,-27,-30,-33,-36,-39,-42,...) - razão r = -3
Progressão aritmética de segunda ordem
Uma progressão aritmética de segunda ordem é considerada por muitos matemáticos o tipo de progessão aritmética mais complexo. Consiste numa sequência de números que, aparentemente, nada parece com uma progressão aritmética, porém percebe-se que a diferença entre os números da sequência cresce em progressão aritmética como mostra o exemplo:
- Sequência - (1,3,7,13,21,31,43,57,73bnk)
Se subtrairmos o primeiro termo da sequência do segundo, teremos como resultado o número 2. Já a diferença entre o segundo e terceiro termos é igual a 4, a diferença entre o terceiro e o quarto termos é igual a 6 e assim sucessivamente. Verificamos que a diferença entre os termos da sequência cresce em progressão aritmética de razão igual a 2.
quinta-feira, 7 de abril de 2011
Função Exponencial
Toda relação de dependência, onde uma incógnita depende do valor da outra, é denominada função. A função denominada como exponencial possui essa relação de dependência e sua principal característica é que a parte variável representada por x se encontra no expoente. Observe:
y = 2 x
y = 3 x + 4
y = 0,5 x
y = 4 x
A lei de formação de uma função exponencial indica que a base elevada ao expoente x precisa ser maior que zero e diferente de um, conforme a seguinte notação:
f: R→R tal que y = a x, sendo que a > 0 e a ≠ 1.
Uma função pode ser representada através de um gráfico, e no caso da exponencial, temos duas situações: a > 0 e 0 < a < 1. Observe como os gráficos são constituídos respeitando as condições propostas:
y = 2 x
y = 3 x + 4
y = 0,5 x
y = 4 x
A lei de formação de uma função exponencial indica que a base elevada ao expoente x precisa ser maior que zero e diferente de um, conforme a seguinte notação:
f: R→R tal que y = a x, sendo que a > 0 e a ≠ 1.
Uma função pode ser representada através de um gráfico, e no caso da exponencial, temos duas situações: a > 0 e 0 < a < 1. Observe como os gráficos são constituídos respeitando as condições propostas:

Uma função exponencial é utilizada na representação de situações onde a taxa de variação é considerada grande, por exemplo, em rendimentos financeiros capitalizados por juros compostos, no decaimento radioativo de substâncias químicas, desenvolvimento de bactérias e micro-organismos, crescimento populacional entre outras situações. As funções exponenciais devem ser resolvidas utilizando, se necessário, as regras envolvendo potenciação.
Vamos apresentar alguns exemplos envolvendo o uso de funções exponenciais.
Exemplo 1
(Unit-SE) Uma determinada máquina industrial se deprecia de tal forma que seu valor, t anos após a sua compra, é dado por v(t) = v0 * 2 –0,2t, em que v0 é uma constante real. Se, após 10 anos, a máquina estiver valendo R$ 12 000,00, determine o valor que ela foi comprada.
Temos que v(10) = 12 000, então:
v(10) = v0 * 2 –0,2*10
12 000 = v0 * 2 –2
12 000 = v0 * 1/4
12 000 : 1/ 4 = v0
v0 = 12 000 * 4
v0 = 48 000
A máquina foi comprada pelo valor de R$ 48 000,00.
Vamos apresentar alguns exemplos envolvendo o uso de funções exponenciais.
Exemplo 1
(Unit-SE) Uma determinada máquina industrial se deprecia de tal forma que seu valor, t anos após a sua compra, é dado por v(t) = v0 * 2 –0,2t, em que v0 é uma constante real. Se, após 10 anos, a máquina estiver valendo R$ 12 000,00, determine o valor que ela foi comprada.
Temos que v(10) = 12 000, então:
v(10) = v0 * 2 –0,2*10
12 000 = v0 * 2 –2
12 000 = v0 * 1/4
12 000 : 1/ 4 = v0
v0 = 12 000 * 4
v0 = 48 000
sábado, 2 de abril de 2011
FUNÇÃO COMPOSTA
determinação de uma terceira função C, formada pela junção das funções A e B. Matematicamente falando, temos que f: A → B e g: B → C, denomina a formação da função composta de g com f, h: A → C. Dizemos função g composta com a função f, representada por gof.
Exemplo 1
Ao considerarmos as funções f(x) = 4x e g(x) = x² + 5, determinaremos:
a) g o f
(g o f)(x) = g(f(x))
g(x) = x² + 5
g(4x) = (4x)² + 5
g(4x) = 16x² + 5
(g o f)(x) = g(f(x)) = 16x² + 5
b) f o g
(f o g)(x) = f(g(x))
f(x) = 4x
f(x² + 5) = 4 * (x² + 5)
f(x² + 5) = 4x² + 20
(f o g)(x) = f(g(x)) = 4x² + 20
Exemplo 2
Vamos determinar g(f(x)) e f(g(x)), em relação às funções f(x) = x + 2 e g(x) = 4x² – 1.
(g o f)(x) = g(f(x))
g(x) = 4x² – 1
g(x + 2) = 4 * (x + 2)² – 1
g(x + 2) = 4 * (x + 2) * (x + 2) – 1
g(x + 2) = 4 * (x² + 2x + 2x + 4) – 1
g(x + 2) = 4 * (x² + 4x + 4) – 1
g(x + 2) = 4x² + 16x + 16 – 1
g(x + 2) = 4x² + 16x + 15
(g o f)(x) = g(f(x)) = 4x² + 16x + 15
(f o g)(x) = f(g(x))
f(x) = x + 2
f(4x² – 1) = (4x² – 1) + 2
f(4x² – 1) = 4x² – 1 + 2
f(4x² – 1) = 4x² + 1
(f o g)(x) = f(g(x)) = 4x² + 1
1 - FUNÇÃO INVERSA
Dada uma função f : A ® B , se f é bijetora , então define-se a função inversa f -1 como sendo a função de B em A , tal que f -1 (y) = x .
Veja a representação a seguir:
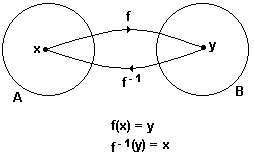
É óbvio então que:
a) para obter a função inversa , basta permutar as variáveis x e y .
b) o domínio de f -1 é igual ao conjunto imagem de f .
c) o conjunto imagem de f -1 é igual ao domínio de f .
d) os gráficos de f e de f -1 são curvas simétricas em relação à reta y = x ou seja , à bissetriz do primeiro quadrante .
Exemplo:
Determine a INVERSA da função definida por y = 2x + 3.
Permutando as variáveis x e y, fica: x = 2y + 3
Explicitando y em função de x, vem:
2y = x - 3 \ y = (x - 3) / 2, que define a função inversa da função dada.
O gráfico abaixo, representa uma função e a sua inversa.
Observe que as curvas representativas de f e de f-1, são simétricas em relação à reta
y = x, bissetriz do primeiro e terceiro quadrantes.
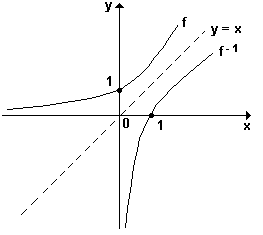
Exercício resolvido:
A função f: R ® R , definida por f(x) = x2 :
a) é inversível e sua inversa é f -1 (x) = Ö x
b) é inversível e sua inversa é f -1(x) = - Ö x
c) não é inversível
d) é injetora
e) é bijetora
SOLUÇÃO:
Já sabemos que somente as funções bijetoras são inversíveis, ou seja, admitem função inversa. Ora, a função f(x) = x2, definida em R - conjunto dos números reais - não é injetora, pois elementos distintos possuem a mesma imagem. Por exemplo,
f(3) = f(-3) = 9. Somente por este motivo, a função não é bijetora e, em conseqüência, não é inversível.
Observe também que a função dada não é sobrejetora, pois o conjunto imagem da função f(x) = x2 é o conjunto R + dos números reais não negativos, o qual não coincide com o contradomínio dado que é
igual a R. A alternativa correta é a letra C.
2 - FUNÇÃO COMPOSTA
Chama-se função composta ( ou função de função ) à função obtida substituindo-se a variável independente x , por uma função.
Simbologia : fog (x) = f(g(x)) ou gof (x) = g(f(x)) .
Veja o esquema a seguir:
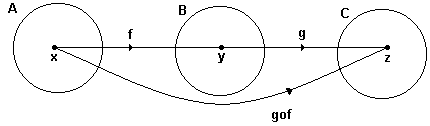
Obs : atente para o fato de que fog ¹ gof , ou seja, a operação " composição de funções " não é comutativa .
Exemplo:
Dadas as funções f(x) = 2x + 3 e g(x) = 5x, pede-se determinar gof(x) e fog(x).
Teremos:
gof(x) = g[f(x)] = g(2x + 3) = 5(2x + 3) = 10x + 15
fog(x) = f[g(x)] = f(5x) = 2(5x) + 3 = 10x + 3
Observe que fog ¹ gof .
Exercícios resolvidos:
1 - Sendo f e g duas funções tais que: f(x) = ax + b e g(x) = cx + d . Podemos afirmar que a igualdade gof(x) = fog(x) ocorrerá se e somente se:
a) b(1 - c) = d(1 - a)
b) a(1 - b) = d(1 - c)
c) ab = cd
d) ad = bc
e) a = bc
SOLUÇÃO:
Teremos:
fog(x) = f[g(x)] = f(cx + d) = a(cx + d) + b \ fog(x) = acx + ad + b
gof(x) = g[f(x)] = g(ax + b) = c(ax + b) + d \ gof(x) = cax + cb + d
Como o problema exige que gof = fog, fica:
acx + ad + b = cax + cb + d
Simplificando, vem:
ad + b = cb + d
ad - d = cb - b \ d(a - 1) = b(c - 1), que é equivalente a d(a - 1) = b(c - 1), o que nos leva a concluir que a alternativa correta é a letra A. .
2 - Sendo f e g duas funções tais que fog(x) = 2x + 1 e g(x) = 2 - x então f(x) é:
a) 2 - 2x
b) 3 - 3x
c) 2x - 5
*d) 5 - 2x
e) uma função par.
SOLUÇÃO:
Sendo fog(x) = 2x + 1, temos: f[g(x)] = 2x + 1
Substituindo g(x) pelo seu valor, fica: f(2 - x) = 2x + 1
Fazendo uma mudança de variável, podemos escrever 2 - x = u, sendo u a nova variável. Portanto, x = 2 - u.
Substituindo, fica:
f(u) = 2(2 - u) + 1 \ f(u) = 5 - 2u
Portanto, f(x) = 5 - 2x , o que nos leva à alternativa D.
Agora resolva esta:
Dadas as funções f(x) = 4x + 5 e g(x) = 2x - 5k, ocorrerá gof(x) = fog(x) se e somente se k for igual a:
*a) -1/3
b) 1/3
c) 0
d) 1
e) -1
Exemplo 1
Ao considerarmos as funções f(x) = 4x e g(x) = x² + 5, determinaremos:
a) g o f
(g o f)(x) = g(f(x))
g(x) = x² + 5
g(4x) = (4x)² + 5
g(4x) = 16x² + 5
(g o f)(x) = g(f(x)) = 16x² + 5
b) f o g
(f o g)(x) = f(g(x))
f(x) = 4x
f(x² + 5) = 4 * (x² + 5)
f(x² + 5) = 4x² + 20
(f o g)(x) = f(g(x)) = 4x² + 20
Exemplo 2
Vamos determinar g(f(x)) e f(g(x)), em relação às funções f(x) = x + 2 e g(x) = 4x² – 1.
(g o f)(x) = g(f(x))
g(x) = 4x² – 1
g(x + 2) = 4 * (x + 2)² – 1
g(x + 2) = 4 * (x + 2) * (x + 2) – 1
g(x + 2) = 4 * (x² + 2x + 2x + 4) – 1
g(x + 2) = 4 * (x² + 4x + 4) – 1
g(x + 2) = 4x² + 16x + 16 – 1
g(x + 2) = 4x² + 16x + 15
(g o f)(x) = g(f(x)) = 4x² + 16x + 15
(f o g)(x) = f(g(x))
f(x) = x + 2
f(4x² – 1) = (4x² – 1) + 2
f(4x² – 1) = 4x² – 1 + 2
f(4x² – 1) = 4x² + 1
(f o g)(x) = f(g(x)) = 4x² + 1
1 - FUNÇÃO INVERSA
Dada uma função f : A ® B , se f é bijetora , então define-se a função inversa f -1 como sendo a função de B em A , tal que f -1 (y) = x .
Veja a representação a seguir:
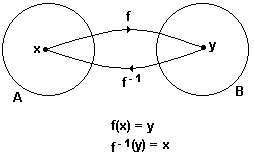
É óbvio então que:
a) para obter a função inversa , basta permutar as variáveis x e y .
b) o domínio de f -1 é igual ao conjunto imagem de f .
c) o conjunto imagem de f -1 é igual ao domínio de f .
d) os gráficos de f e de f -1 são curvas simétricas em relação à reta y = x ou seja , à bissetriz do primeiro quadrante .
Exemplo:
Determine a INVERSA da função definida por y = 2x + 3.
Permutando as variáveis x e y, fica: x = 2y + 3
Explicitando y em função de x, vem:
2y = x - 3 \ y = (x - 3) / 2, que define a função inversa da função dada.
O gráfico abaixo, representa uma função e a sua inversa.
Observe que as curvas representativas de f e de f-1, são simétricas em relação à reta
y = x, bissetriz do primeiro e terceiro quadrantes.
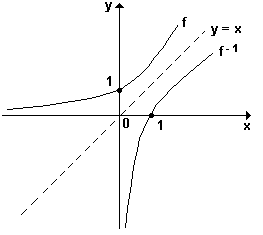
Exercício resolvido:
A função f: R ® R , definida por f(x) = x2 :
a) é inversível e sua inversa é f -1 (x) = Ö x
b) é inversível e sua inversa é f -1(x) = - Ö x
c) não é inversível
d) é injetora
e) é bijetora
SOLUÇÃO:
Já sabemos que somente as funções bijetoras são inversíveis, ou seja, admitem função inversa. Ora, a função f(x) = x2, definida em R - conjunto dos números reais - não é injetora, pois elementos distintos possuem a mesma imagem. Por exemplo,
f(3) = f(-3) = 9. Somente por este motivo, a função não é bijetora e, em conseqüência, não é inversível.
Observe também que a função dada não é sobrejetora, pois o conjunto imagem da função f(x) = x2 é o conjunto R + dos números reais não negativos, o qual não coincide com o contradomínio dado que é
igual a R. A alternativa correta é a letra C.
2 - FUNÇÃO COMPOSTA
Chama-se função composta ( ou função de função ) à função obtida substituindo-se a variável independente x , por uma função.
Simbologia : fog (x) = f(g(x)) ou gof (x) = g(f(x)) .
Veja o esquema a seguir:

Obs : atente para o fato de que fog ¹ gof , ou seja, a operação " composição de funções " não é comutativa .
Exemplo:
Dadas as funções f(x) = 2x + 3 e g(x) = 5x, pede-se determinar gof(x) e fog(x).
Teremos:
gof(x) = g[f(x)] = g(2x + 3) = 5(2x + 3) = 10x + 15
fog(x) = f[g(x)] = f(5x) = 2(5x) + 3 = 10x + 3
Observe que fog ¹ gof .
Exercícios resolvidos:
1 - Sendo f e g duas funções tais que: f(x) = ax + b e g(x) = cx + d . Podemos afirmar que a igualdade gof(x) = fog(x) ocorrerá se e somente se:
a) b(1 - c) = d(1 - a)
b) a(1 - b) = d(1 - c)
c) ab = cd
d) ad = bc
e) a = bc
SOLUÇÃO:
Teremos:
fog(x) = f[g(x)] = f(cx + d) = a(cx + d) + b \ fog(x) = acx + ad + b
gof(x) = g[f(x)] = g(ax + b) = c(ax + b) + d \ gof(x) = cax + cb + d
Como o problema exige que gof = fog, fica:
acx + ad + b = cax + cb + d
Simplificando, vem:
ad + b = cb + d
ad - d = cb - b \ d(a - 1) = b(c - 1), que é equivalente a d(a - 1) = b(c - 1), o que nos leva a concluir que a alternativa correta é a letra A. .
2 - Sendo f e g duas funções tais que fog(x) = 2x + 1 e g(x) = 2 - x então f(x) é:
a) 2 - 2x
b) 3 - 3x
c) 2x - 5
*d) 5 - 2x
e) uma função par.
SOLUÇÃO:
Sendo fog(x) = 2x + 1, temos: f[g(x)] = 2x + 1
Substituindo g(x) pelo seu valor, fica: f(2 - x) = 2x + 1
Fazendo uma mudança de variável, podemos escrever 2 - x = u, sendo u a nova variável. Portanto, x = 2 - u.
Substituindo, fica:
f(u) = 2(2 - u) + 1 \ f(u) = 5 - 2u
Portanto, f(x) = 5 - 2x , o que nos leva à alternativa D.
Agora resolva esta:
Dadas as funções f(x) = 4x + 5 e g(x) = 2x - 5k, ocorrerá gof(x) = fog(x) se e somente se k for igual a:
*a) -1/3
b) 1/3
c) 0
d) 1
e) -1
quinta-feira, 24 de março de 2011
Criado por René Descartes, o plano cartesiano consiste em dois eixos perpendiculares, sendo o horizontal chamado de eixo das abscissas e o vertical de eixo das ordenadas. O plano cartesiano foi desenvolvido por Descartes no intuito de localizar pontos num determinado espaço. As disposições dos eixos no plano formam quatro quadrantes, mostrados na figura a seguir:
O encontro dos eixos é chamado de origem. Cada ponto do plano cartesiano é formado por um par ordenado (x , y ), onde x: abscissa e y: ordenada.
Marcando pontos no plano cartesiano
Dados os pontos A(3,6), B(2,3), C(-1,2), D(-5,-3), E(2,-4), F(3,0), G(0,5), represente-os no plano cartesiano.
Marcando o ponto A(3,6)
Primeiro: localiza-se o ponto 3 no eixo das abscissas
Segundo: localiza-se o ponto 6 no eixo das ordenadas
Terceiro: Traçar a reta perpendicular aos eixos, o encontro delas será o local do ponto.
trabalhos relacionados à cartografia, localizações geográficas, pontos estratégicos de bases militares, localizações no espaço aéreo, terrestre e marítimo.
Por Marcos Noé
Graduado em Matemática
Equipe Brasil Escola
Equipe Brasil Escola
Assinar:
Postagens (Atom)



